letvasup.blogg.se - Moment of inertia of a circle about x axis

#Moment of inertia of a circle about x axis full#
#Moment of inertia of a circle about x axis plus#

The radius of revolution about an axis 12 cm away from the center of mass of a body of mass 1.2 kg is 13 cm. Question.10. The moment of inertia of a circular section about an axis perpendicular to the section isġ. Then the moment of inertia of the body about the axis of rotation.

Question.9. The moment of inertia of a circular section of base ‘b’ and height ‘h’ about an axis passing through its vertex and parallel to base is Question.8. The moment of inertia of a body is always minimum with respect to its The moment of inertia of a triangular section of base ‘b’ and height ‘h’ about an axis passing through its base is ………. times the moment of inertia about an axis passing through its C.G. Question.6. The polar moment of inertia of a circular section is about The moment of inertia of a triangular section of base ‘b’ and height’h’ about an axis passing through its C.G. The moment of inertia of a circular section of diameter ‘d’ about its centroidal axis is given by The moment of inertia of a rectangle base ‘b’ and depth ‘d’ about the base will be Question.2. The unit of moment of inertia is The polar moment of inertia of a circular section is about (a) X-X axis (b) Y-Y axis (c) Z-Z axis (d) Neutral axis. and parallel to the base is (a) (b) (c) (d) Question.6. (d) Depends upon the shape of the section The moment of inertia of a triangular section of base ‘b’ and height’h’ about an axis passing through its C.G. 3 provides the moment of inertia and section modulus formula for common geometrical shapes.(c) Depends upon the dimensions of the section I total 1 3 m r L 2 + 1 2 m d R 2 + m d ( L + R) 2. Determine: the moment of inertia of the composite.

#Moment of inertia of a circle about x axis plus#

Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted axis of rotation, we find the moment of inertia for the compound object to be. Ix moment of inertia about axis x-x (in 4) Ic moment of inertia about the centroidal axis c-c parallel to x-x (in 4) A area of the section (in 2) d perpendicular distance between the parallel axes x-x and c-c (in) Transfer Formula Given: the glued asymmetric built-up cross-section below. I parallel-axis 1 2 m d R 2 + m d ( L + R) 2. Th t fi ti fth hdd iThe moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle Determine the moment of inertia of the shaded area with respect to the x axis. I parallel-axis 1 2 m d R 2 + m d ( L + R) 2. In SI unit systems the unit of Section Modulus is m 3 and in US unit system inches 3. bounding rectangle and half-circle with respect to the x axis. Section modulus is denoted by “Z” and mathematically expressed as Z=I/y Moment of Inertia Formula for Square Cross-Section: The moment of inertia equation for a square is given by I x I y a 4 /12 where alength of side. Section modulus of a section is defined as the ratio of moment of inertia (I) to the distance (y) of extreme fiber from the neutral axis in that section. The larger the moment of inertia, the greater is the moment of resistance against bending. Bending stresses are inversely proportional to the Moment of Inertia.

A moment of inertia is required to calculate the Section Modulus of any cross-section which is further required for calculating the bending stress of a beam.

The Critical Axial load, Pcr is given as P cr= π 2EI/L 2.

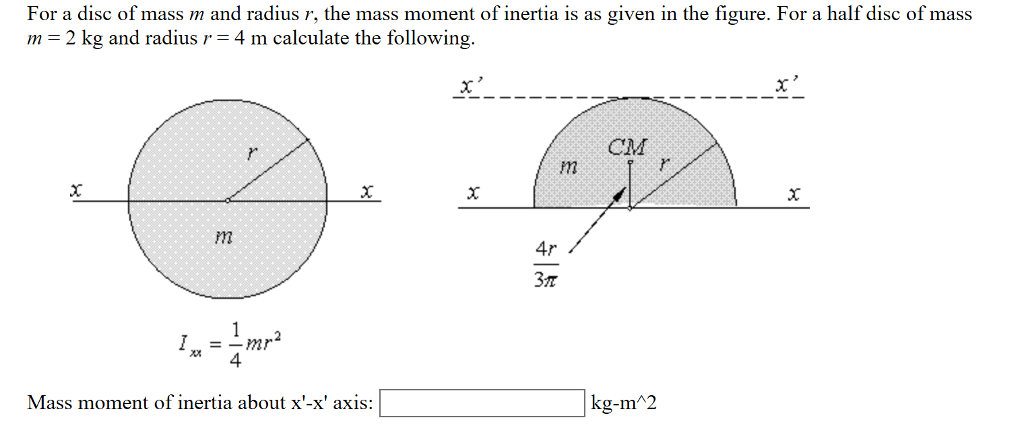
Calculate the moment of inertia of the shape given in the following figure, around a horizontal axis x-x that is passing through centroid.

The moment of inertia “I” is a very important term in the calculation of Critical load in Euler’s buckling equation. This is the wanted moment of inertia of the composite area around axis x-x.

Polar moment of inertia is required in the calculation of shear stresses subject to twisting or torque.

Area moment of inertia is the property of a geometrical shape that helps in the calculation of stresses, bending, and deflection in beams.

With that, we will solve the equation below. However, the part of the circle rotating about an axis will be symmetric and the values will be equal for both the y and x-axis. Thus similarly for the semicircle, the moment of inertia of the x-axis is equal to that of the y-axis.

#Moment of inertia of a circle about x axis full#

Mass moment of inertia provides a measure of an object’s resistance to change in the rotation direction. Now if take a quarter circle, the moment of inertia relative to the x-axis and y-axis will be one quarter the moment inertia of a full circle. We know that for a full circle because of complete symmetry and uniform area distribution, the moment of inertia relative to the x-axis is equal to that of the y-axis.